A simple Deep Neural Network, from scratch.

This project was an assignment in a neural-computation course called Introduction to Neural Networks. We studied computational models of the brain and followed their mathematical models. Instances of the network had their weights and biases trained to solve various problems, such as recognizing MNIST digits.

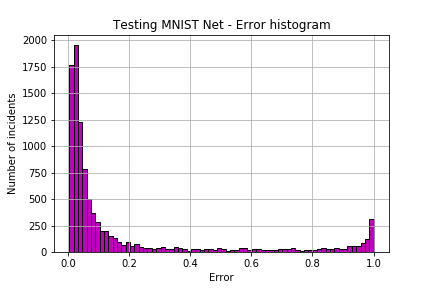
I thoroughly enjoyed programming a dynamic Feed-Forward network in NumPy! Seeing the algorithm at work was a blast! We can observe the algorithm’s results in the following picture. It was trained to recognize MNIST digits, and the histogram shows that most incidents had a near-zero error!

Algorithm Walkthrough

The code followed the mathematical backpropagation algorithm (based on gradient descent) in J. Hertz’s Introduction to Neural Computation book:

Below is an overview of the algorithm and snippets of the code used. For a detailed report, refer to this link and for the Python code, visit here.

Feedforward Computation

The feedforward process involves passing inputs through the network to produce outputs. Each layer performs a weighted sum of inputs followed by an activation function. The output of one layer becomes the input for the next. In the code, the feedforward function performs this operation.

Input Layer:
- The input (a) is augmented with a bias neuron (always set to 1) and stored in the network.
```
a = np.append(a, 1)
self.network.append(a)
```
Hidden Layers:
- For each hidden layer (m):
  - A bias term is added to the layer’s input.
```
b = np.zeros(self.sizes[m] + 1)
b[-1] = 1
```
  - The activation of each neuron in the layer is computed using the sigmoid function.
```
for i in range(self.sizes[m]):
    b[i] = g(np.dot(a, W[:, i]))
```
  - The result becomes the input for the next layer, and the activation is stored in the network.
```
self.network.append(b)
a = np.copy(b)
```
- The final activation (a) is returned.

Backpropagation

Backpropagation is the process of updating the weights of the neural network to minimize the error between the predicted and actual outputs. The algorithm works backward from the output layer to the input layer, adjusting weights based on the computed error gradients.

The backProp function in the code executes backpropagation:

Output Layer Error:

Calculate the error in the output layer using the derivative of the sigmoid function.

for i in range(self.sizes[-1]):
    self.deltas[-1][i] = g_prime(np.dot(self.network[-2], W[:, i])) * (expected[i] - output[i])

Hidden Layer Error:

For each hidden layer (m) from the output layer to the second layer:

Compute the error term for each neuron in the layer.

for j in range(self.sizes[m-1] + 1):
    h_prev = np.dot(self.network[m-2], W_prev[:, j])
    h = np.dot(W[j, :], self.deltas[m])
    self.deltas[m-1][j] = g_prime(h_prev) * h

Weight Update:

Update the weights using the computed error terms, the learning rate (step), and the activations.

for m in range(1, self.num_layers):
    W = self.weights[m-1]
    for i in range(np.shape(W)[1]):
        W[:, i] += self.step * self.network[m-1] * self.deltas[m][i]

These steps are essential for the network to learn from the training data and adjust its weights to improve its performance over time. The learning rate (step) controls the size of the weight updates, influencing the convergence and stability of the training process.

The provided Python code encapsulates these fundamental concepts of feedforward computation and backpropagation, which are core components of training neural networks.